기술 자료실

Lambert의 코사인 법칙 (Lambert’s Cosine Law)

적외선 방출에서 각도 의존성

Lambert의 코사인 법칙은, 열평형 상태에 있는 흑체에서 방출되는 복사가 모든 방향으로 동일하게 방출되지만, 투영 효과로 인해 각도에서는 약하게 보인다고 말합니다. 이 법칙은 이상적인 난반사체(ideal diffuse radiator)에서 관측되는 방사 강도가 적외선 센서의 시선과 표면 법선 사이의 각도의 코사인 값에 비례한다는 것을 나타냅니다. 작은 표면 영역에서 방출되는 복사 플럭스는 표면 법선에 대한 방출 각 θ에 따라 코사인에 비례하여 감소합니다. 이는 표면에 수직으로(θ = 0) 최대 방사가 일어나고, 각도가 커질수록 겉보기 방출 면적이 cos(θ)에 비례해 감소함을 의미합니다. 흑체는 모든 방향으로 균일하게 복사를 방출하므로, 스펙트럼 복사 밝기(spectral radiance)는 일정하지만, 관측되는 강도는 투영 효과에 따라 달라집니다. 단위 면적에서 방출되는 전체 전력은 스펙트럼 복사 밝기가 투영된 방출 면적을 고려하여 표현할 수 있습니다.

이 방정식에서, 미소 입체각 dΩ는 복사가 방출되거나 측정되는 입체각의 작은 부분을 나타냅니다. 이는 복사의 방향성을 설명하며, 단위는 스테라디안(sr)입니다. 미소 표면적 dA는 방출 표면의 극히 작은 면적을 의미하며, 흑체 또는 방출 표면의 극히 일부가 방사에 기여함을 나타냅니다. 미소 파장 대역 dλ는 방출 스펙트럼 내의 작은 파장 간격을 가리킵니다.

대부분의 비도전성(nonconducting) 표면은 난반사(diffuse) 또는 "Lambertian"으로 간주할 수 있습니다. 이는 Lambertian 표면에서 스펙트럼 복사 밝기 Bλ(T)와 스펙트럼 방사 강도 Iλ(T)가 수치적으로 동일함을 의미합니다. 스펙트럼 방사 전력 M∘(T)는 단위 면적당, 단위 파장당 흑체가 모든 반구 방향으로 방출하는 전체 전력을 나타냅니다.

Iλ=Bλ(T)=M°(T)/Iλ=Bλ(T)=M°(T)/π

방사 강도 I 관점에서, 표면 법선에 대해 θ 각도로 바라볼 때의 방사 강도 Iθ와 표면에 수직 방향에서 최대 방사 강도 I⊥는 다음과 같이 표현됩니다.

Iθ=  I⊥cos(θ)

이 법칙은 코사인 방출 법칙(cosine emission law)이라고도 불립니다. 그림 1은 흑체에 대한 이 관계를 보여줍니다.

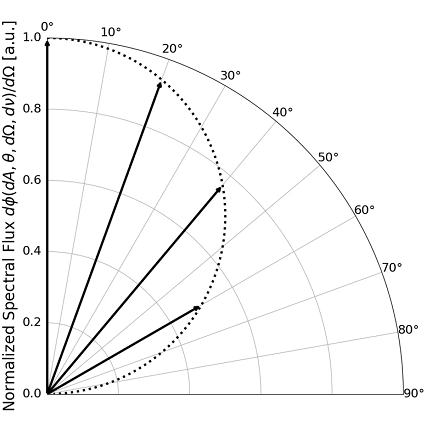
이 법칙은 이론과 경험적 관찰에 기반하며, 표면이 거울 반사(specular)가 아님을 가정합니다. 파장이 길어질수록 주어진 재료 표면이 Lambertian으로 간주될 가능성이 줄어듭니다. 이는 대부분의 표면이 연마되지 않은 경우, 파장 규모에서 “거칠다(rough)”고 간주되기 때문입니다. 따라서 센서가 표면을 각도에서 관측할 경우, 방사 강도는 표적과 센서 사이의 각도의 코사인 값에 따라 감소합니다. 또한 거울 표면은 이 법칙을 따르지 않고, 기하광학(geometrical optics)의 스넬 법칙(Snell’s law)을 따릅니다.

요약

- 코사인 법칙은 방사선이 표면 면적, 각도, 파장에 따라 어떻게 퍼지는지 설명하며, 적외선 센서 및 열 이미징에서 중요한 역할을 합니다.

- 흑체는 모든 방향으로 방사하지만, 각도에서는 표면 면적 투영 때문에 약하게 보입니다.

- 최대 방사는 표면에 수직(θ = 0)으로 방출되며, 각도가 커질수록 방사 강도는 감소합니다.

출처

- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653

- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics rules of thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485

- De Witt, Nutter: Theory and Practice of Radiation Thermometry, 1988, John Wiley & Son, New York, https://doi.org/10.1002/9780470172575