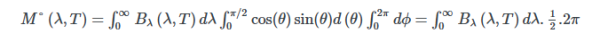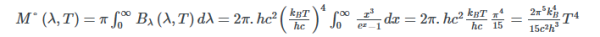기술 자료실

플랑크 법칙에서 스테판–볼츠만 법칙까지 From Planck’s Law to Stefan–Boltzmann

네제곱 온도 의존성

슈테판–볼츠만 법칙(Stefan–Boltzmann law)은 슈테판의 법칙이라고도 하며, 열적 평형 상태에 있는 흑체가 단위 표면적당 방출하는 총 에너지를 정의하는 법칙입니다. 어떤 물체에서 방출되는 총 복사 전력을 구하기 위해서는 복사 방출률에 그 물체의 표면적 A를 곱하면 됩니다. 이 법칙은 복사 방출률 M을 온도의 함수로 나타냅니다. 복사 방출률에 원 모양의 위첨자가 붙어 있는 경우, 이는 흑체에만 해당하는 물리량임을 의미합니다.

M(T) = ε M∘(T)= ε σ T4 

비례 상수 σ는 슈테판–볼츠만 상수(Stefan–Boltzmann constant)라고 불리며, 이는 기본적인 물리 상수들로부터 유도된 값입니다.

일반적인 경우에서 슈테판–볼츠만 법칙은 복사를 방출하는 표면의 방사율을 포함한 복사 방출률의 형태로 표현됩니다. 회색체의 경우, 면적 A에서 방출되는 복사 전력 P는 방사율 ε에 의해 보정되며, 이 방사율은 물질이 적외선을 방출하는 능력을 반영합니다.

P(T)=AM(T)=A.ϵ.σ.T4

이 법칙은 플랑크의 법칙을 전체 스펙트럼과 반구 영역에 대해 적분하고 램버트의 코사인 법칙을 고려하여 유도할 수 있습니다. 여기서 Bλ​(λ,T)는 플랑크 법칙으로부터 얻은 복사 스펙트럼이고, $\Omega =\sin (\theta )d\theta d\varphi$는 구면 좌표계에서의 입체각 요소를 나타냅니다. $\theta$는 표면 법선과 복사 방향 사이의 각도이며,$\varphi$는 반구 영역 내 방향의 각도입니다. 또한 $\cos (\theta )$ 항은 램버트의 코사인 법칙을 고려한 것입니다.

M(λ,T)=∫∞0∫Bλ(λ,T)cos(σ)dΩ dλ

Bλ​(λ,T)는 방향에 독립적이므로, 반구에 대한 각도 적분은 삼각함수 항의 적분이 단순한 π 인수로 정리됩니다.

스펙트럼 복사도 Bλ​(λ,T)를 적분할 때는 지수 항을 x=λkB​Thc​로 치환해야 하며, 이때 dλ =−λ2kB​Th​dx가 됩니다. 또한 보스-아인슈타인 적분(Bose-Einstein integral)을 고려하면, 이 방정식은 다음과 같이 단순화됩니다.

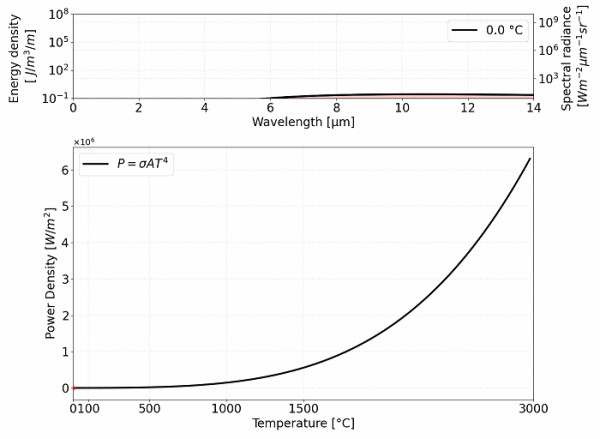
마지막 항은 이미 소개된 스테판–볼츠만 상수를 나타내며, 흑체가 방출하는 에너지가 온도의 네제곱에 비례함을 보여줍니다. 그림 1은 방출 스펙트럼과 방출 전력 사이의 관계를 나타냅니다.

그림1. 흑체 표면에서 단위 면적당 방출되는 총 전력(P)은 온도의 네제곱에 비례한다.

요약

- 스테판–볼츠만 법칙은 흑체가 단위 면적당 방출하는 총 에너지가 그 온도의 네제곱에 비례한다고 명시한다.

- 이 법칙은 플랑크의 복사 법칙에서 유도되며, 여기서 스펙트럼 복사휘도를 모든 파장과 모든 방향에 대해 적분하고 램버트 코사인 법칙을 고려한다.

출처

- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653

- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics rules of thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485

- De Witt, Nutter: Theory and Practice of Radiation Thermometry, 1988, John Wiley & Son, New York, https://doi.org/10.1002/9780470172575