기술 자료실

적외선 측정에서의 방사율 Emissivity in Infrared Measurement

파장, 각도, 온도에 따른 영향

방사율은 적외선 온도 측정에서 기본적인 특성으로, 물체가 이상적인 흑체에 비해 얼마나 효율적으로 적외선을 방출하는지를 정의합니다. 방사율 값은 0에서 1 사이이며, 재질이 흑체 대비 얼마나 열복사를 방출하는지를 수치로 나타냅니다. 방사량(emittance)은 표면의 실제 복사 에너지 출력으로, 온도와 재질 의존적인 방사율에 의해 영향을 받습니다.

흑체(Blackbody)는 이상화된 물체로, 모든 입사 방사선을 반사나 투과 없이 흡수하며, 모든 파장에서 가능한 최대 에너지를 방출합니다. 흑체의 방사 분포는 방향과 무관합니다. 하지만 실제 재료는 거의 이상적인 흑체와 일치하지 않습니다. 회색체(Gray body)는 동일 온도에서 훨씬 적은 복사를 방출합니다. 재질이 모든 파장에서 일정한 방사율을 가지면 이를 회색체라고 하지만, 이는 자연에서 거의 발생하지 않습니다.

방사율은 스펙트럼 특성과 방향 특성에 따라 분류됩니다.

과학적으로, 반구 평균 방사율 εh는 표면의 복사 방사량 Mλ(λ,T)와 동일 온도의 흑체 복사 방사량 Mλ°(λ,T) 비율로 정의됩니다. 방사율은 특정 파장, 방향, 편광 상태에 대해 정의할 수 있습니다.

방향성 방사율은 적외선 온도 측정에서 중요한 파라미터입니다. 적외선 카메라와 적외선 온도계는 모든 방향에서가 아니라 특정 방향에서 방출되는 복사를 감지하기 때문입니다. 대부분의 장치는 표면에 수직으로 입사하는 방사율 값을 가정하며, 수직 측정이 가장 정확합니다. 각도에서 측정할 경우, 관측 각도에 따른 방사율 변화를 고려해야 합니다.

열복사에 관한 키르히호프 법칙(Kirchhoff’s Law)에 따르면, 열평형에 있는 표면의 방사율은 같은 파장에서의 흡수율과 같습니다. 표면에 입사한 전체 방사선은 방출, 투과, 반사 중 하나로 나뉘므로, 방사율 관계식은 다음과 같습니다.

ε = 1 − τ − ρ

여기서 τ는 투과율(transmissivity), ρ는 파장별 반사율(reflectivity)입니다. 두께가 충분히 두꺼워 빛이 통과하지 않는 불투명 재료의 경우, 방사율은 단순히

ε = 1 − ρ

로 표현할 수 있습니다.

방사율은 재료의 화학적 조성과 구조에도 영향을 받으며, 재료의 굴절률과 소멸계수(extinction coefficient)와 같은 광학적 파라미터로 평가할 수 있습니다. 소멸계수는 산란과 흡수로 인해 단위 부피당 빛이 감소하는 정도를 나타냅니다. 방사율은 두 개의 직교 편광 성분(S-편광: 입사 평면에 수직, P-편광: 입사 평면에 평행)에 따라 정의되며, 모든 편광 상태는 이 두 성분으로 분해 가능합니다.

복소 굴절률 n = n2 + ik인 두 번째 매질을 고려해야 하며, n1은 1로 단순화할 수 있습니다. 편광 방향에 따라 방사율은 Fresnel 방정식으로 계산되며, 이는 매끄러운 표면에만 적용 가능합니다.

실제 대부분 응용에서는 편광 없는 적외선 방출을 사용하며, 이는 S와 P 편광이 동일하게 분포됨을 의미합니다. 따라서 재질의 유효 방사율은 두 편광의 평균으로 계산할 수 있습니다.

ε= 12(εs + εp)

ε= 12(εs + εp)

εn(ϕ=0°)=(4n1n2)/((n1+n2)2+k2)

로 단순화됩니다.

각 재질은 고유의 방사율 특성을 가지며, 파장에 따라 방사율이 변합니다. 실제 물질은 모든 방향에서 균일하게 방출하지 않으므로, 람베르시안 표면처럼 행동하지 않습니다. 도체와 유전체 재질 간 차이가 존재합니다.

유전체(dielectric)의 경우, 관측 각도가 커질수록 방사율이 감소합니다. 유전체는 전기적으로 절연하며 전기장을 저장할 수 있지만, 에너지 손실은 최소화됩니다. 그림 1은 유전체의 방향성 방사율과 관측 각도 관계를 예시로 보여줍니다. 이 곡선은 유리, 플라스틱, 유기 재료 등 비전도성 재질에도 적용 가능합니다. 매끄러운 유전체 표면의 경우, 굴절률만 방사율에 영향을 미치며, 60°까지 방사율이 거의 일정하고 이후 람베르시안 법칙에 따라 감소합니다.

도체(conductor)의 경우, 특정 각도에서 방사율이 증가하고 이후 람베르시안 법칙에 따라 감소합니다. 60°까지는 거의 일정하지만, 유전체보다 낮은 수준을 유지합니다.

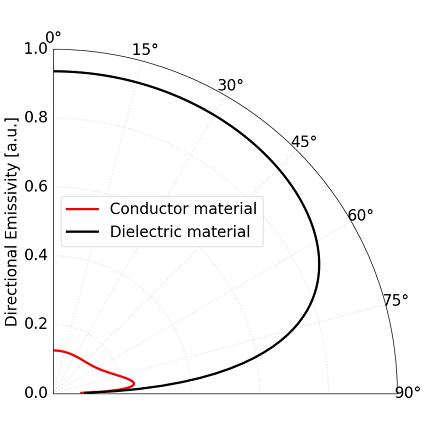
그림1. 유전체 재료(굴절률 n = 1.7, 검은색 곡선)와 도체 재료(굴절률 n = 2.8, 소멸계수 k = 4.4, 빨간색 곡선)의 방사 각도에 따른 예시 방향성 방사율

유전체 재료는 모든 각도에서 높은 방사율을 보이다가, 비스듬한 각도에서는 점차 감소합니다. 반면 도체 재료는 매우 낮은 방사율을 가지며,

반사율이 높기 때문에 큰 각도에서 방사율이 더 감소합니다. 이는 서로 다른 재료 유형에서 방사율이 각도에 따라 크게 달라짐을 보여줍니다.

방사율은 방향에 따라 달라지며 파장에 따라 변하는 특성을 가지는데, 이를 스펙트럼 방사율(spectral emissivity)이라고 합니다. 이러한 변화는 재료가 원자 및 분자 구조에 따라 서로 다른 파장의 적외선과 다르게 상호작용하기 때문에 발생합니다. 열복사의 흡수와 방출은 전자 전이, 진동 모드, 격자 상호작용 등에 의해 결정되며, 이는 파장에 따라 달라집니다. 반사율이 높은 금속과 같은 도체는 긴 적외선 파장에서 낮은 방사율을 가지는 경향이 있습니다. 반면, 세라믹이나 산화물과 같은 유전체는 특정 스펙트럼 영역에서 분자의 진동이 강하게 에너지를 흡수하고 재방출하기 때문에 높은 방사율을 보입니다. 그림 2에서 볼 수 있듯이, 이러한 파장 의존성은 적외선 온도 측정에서 매우 중요한 요소이며, 적절한 스펙트럼 범위를 선택함으로써 특히 적외선 스펙트럼에서 방사율이 다양하게 변하는 재료의 정확한 측정이 가능합니다.

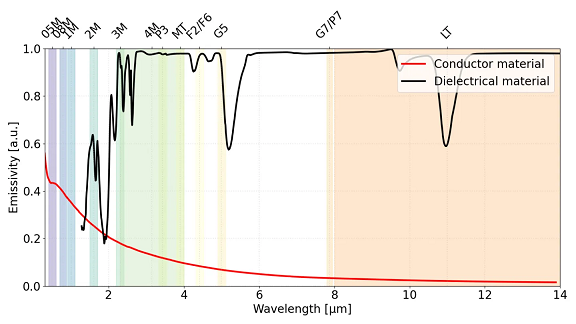
그림2. 정규 입사각에서 도체(빨간색 곡선)와 유전체 재료(검은색 곡선)의 파장에 따른 예시 방향성 방사율

도체는 모든 파장에서 낮은 방사율을 보이며, 파장이 길어질수록 점차 감소하는데, 이는 반사율이 높은 금속 표면의 특성입니다.

반면 유전체 재료는 대부분의 적외선 영역에서 높은 방사율을 보이지만, 특정 파장 범위에서는 투과 또는 반사 효과로 인해 방사율이 낮아집니다.

재료 표면이 거칠어지면, 거친 표면의 미세 구조 내에서 열복사가 여러 번 반사되고 산란되면서 방사율이 증가합니다. 거칠기는 낮은 방사율을 가진 금속에 큰 영향을 미치지만, 이미 방사율이 높은 유전체에는 상대적으로 작은 영향을 줍니다. 매끄러운 표면은 입사 복사를 더 많이 반사하여 흡수되고 방출되는 에너지 양을 줄입니다. 반대로, 거친 표면은 수많은 미세한 공동(cavity)을 형성하여 복사를 가두고, 흡수 및 재방출을 증가시킵니다. 이 효과는 특히 연마된 금속에서 두드러지는데, 금속의 매끄러운 표면은 높은 반사율 때문에 방사율이 낮습니다. 표면 거칠기가 증가하면 방출에 사용되는 유효 표면적이 커져 더 많은 에너지가 방출될 수 있습니다. 또한, 표면 불규칙성은 정반사(specular reflection)를 방해하여 난반사(diffuse reflection)로 변환시키고, 이는 에너지 흡수를 증가시키고 외부 반사로 인한 손실을 줄입니다. 미세한 규모에서는, 거친 표면이 재료의 광학적 성질에도 영향을 미쳐 적외선과의 상호작용 방식을 바꾸기도 합니다. 이러한 흡수 증가, 내부 다중 반사, 그리고 표면적 증가의 결합은 전체 방사율을 높이는 결과를 가져옵니다.

다음 식은 표면 거칠기 RaR_aRa​ (평균선에서 표면 프로파일의 편차를 정량화)와 동일한 재료에서 두 가지 표면 조건 간의 스펙트럼 방사율의 관계를 보여줍니다 [4,5,6]:

ε= (1 + (1ε0 − 1)RaR0)−1

여기서  ε0ε0 는 매끄러운 표면의 방사율을, R0R0는 초기 거칠기를 나타냅니다. 이 식은 방사율이 거칠기와 함께 점근적으로 증가함을 보여줍니다. 표면 거칠기는 처리 방식에 따라 다르며, 거울처럼 연마된 금속은 0.01–0.1 µm, 기계 가공된 금속은 0.1–5 µm, 샷 블라스트 처리된 표면은 5–50 µm에 이릅니다. 코팅 또는 산화된 표면은 0.5–10 µm 범위이며, 주조되거나 부식된 금속은 일반적으로 50 µm를 초과합니다.

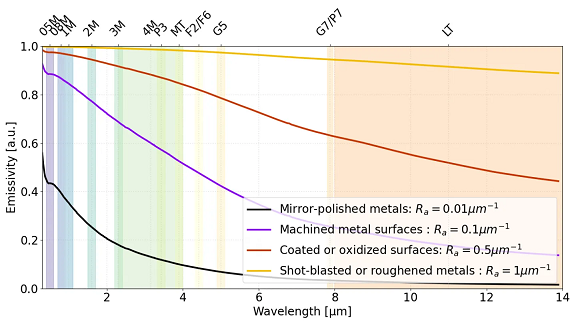
그림3. 다양한 거칠기 수준을 가진 금속 표면의 파장별 방사율 예시. 그래프는 네 가지 표면 상태를 비교합니다:

거울처럼 연마된 금속, 기계 가공된 금속 표면, 코팅 또는 산화된 표면, 그리고 샷 블라스트 처리되거나 거칠어진 표면.

방사율은 온도에 따라서도 달라집니다. 이는 재료의 고유한 광학적 특성이 열적 자극에 의해 변할 수 있기 때문입니다. 온도가 높아지면 전자 밀도, 격자 진동, 상 변화 등이 재료의 열 복사 방출 능력에 영향을 줍니다. 금속의 경우, 온도가 높아지면 자유 전자 산란이 증가해 특정 파장에서 방사율이 높아질 수 있습니다. 유전체나 세라믹은 온도가 상승하면 포논 활동 증가와 밴드갭 흡수 변화로 인해 방사율이 높아지는 경향을 보입니다. 또한, 표면 산화나 고온에서의 구조 변화는 재료의 반사율과 흡수 특성을 바꿔 방사율에 영향을 줄 수 있습니다. 그림 4는 온도 변화에 따라 방사율이 달라지는 대표적인 재료들의 총 방사율 변화를 보여줍니다.

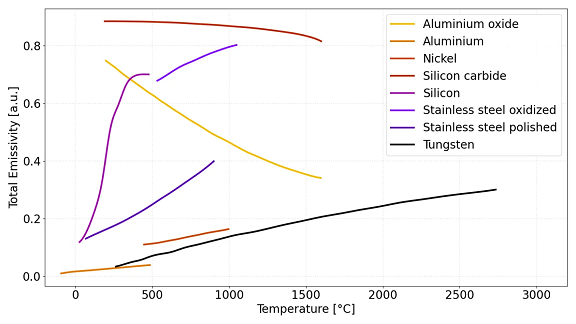
그림4. 다양한 재료, 금속, 산화물, 세라믹의 온도에 따른 총 방사율 변화. 텅스텐(검은색 곡선), 알루미늄(주황색 곡선), 니켈(진한 주황색 곡선)과 같은 금속은

낮은 방사율을 가지며, 온도가 높아질수록 점차 방사율이 증가합니다. 연마된 스테인리스강(진한 보라색 곡선) 역시 낮은 방사율을 보이지만,

산화된 형태(연한 보라색 곡선)는 훨씬 높은 방사율을 나타냅니다. 실리콘 카바이드(빨간색 곡선)와 산화알루미늄(노란색 곡선)과 같은 비금속 재료는 전체 온도 범위에서 높은 방사율을 유지합니다.

재료가 반투명일 경우, 방사율은 재료의 광학적 특성과 두께 모두에 영향을 받습니다. 이는 적외선이 일부 투과하거나 내부에서 반사되기 때문입니다. 매우 얇은 필름에서는 적외선의 상당 부분이 재료를 통과할 수 있어, 실제 방사율이 낮아집니다. 두께가 증가하면 흡수가 더 지배적이 되어 방사율이 높아집니다. 그러나 간섭 효과도 발생할 수 있는데, 특정 파장에서 필름 내에서 보강 간섭이나 상쇄 간섭이 일어나 방사율이 파장에 따라 달라질 수 있습니다. 그림 5는 얇은 플라스틱 필름을 예로 들어, 두께 변화가 재료의 적외선 방출 능력에 어떤 영향을 미치는지 보여줍니다.

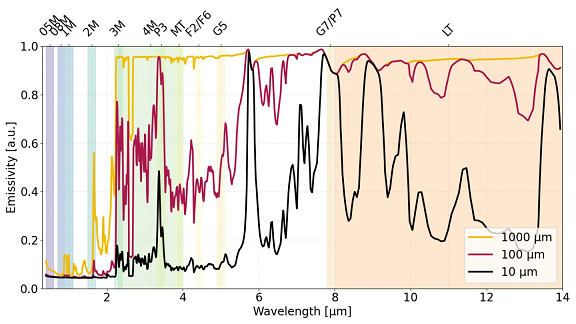
그림 5. 두께가 다른 폴리에틸렌 테레프탈레이트(PET) 필름(10 µm, 100 µm, 1000 µm)의 파장별 방사율.

데이터는 방사율이 파장과 재료 두께 모두에 따라 달라짐을 보여줍니다. 얇은 필름(10 µm, 검은색 곡선)은 일부 투과와 간섭 효과 때문에 방사율이 낮고 파장에 따른 변화가 뚜렷합니다.

두께가 증가함에 따라 방사율은 일반적으로 높아지며, 1000 µm 필름(노란색 곡선)은 불투명에 가까운 특성을 보여 대부분의 파장에서 방사율이 높고 안정적입니다.

요약
- 방사율(Emissivity)은 재료가 완전 흑체(0에서 1 사이 값)에 비해 얼마나 효율적으로 적외선을 방출하는지를 측정합니다.
- 방사율의 종류: 총 방사율(Total, 모든 파장), 단색 방사율(Monochromatic, 특정 파장), 반구 방사율(Hemispherical, 모든 방향), 방향성 방사율(Directional, 특정 각도).
- 실제 재료는 완전한 흑체가 아니며, 회색체(gray body, 방사율이 일정)일 수도 있고 파장이나 방향에 따라 방사율이 달라질 수도 있습니다.
- 영향을 미치는 요인:

   1. 재료 구성(Material composition) (금속은 방사율이 낮고, 유전체(dielectric)는 방사율이 높음)

   2. 표면 거칠기(Surface roughness)는 반사율을 줄여 방사율을 높임

   3. 온도(Temperature)는 일부 재료의 광학적 특성 변화를 통해 방사율에 영향을 줌

   4. 두께(Thickness)는 반투명 재료나 얇은 재료에서 투과와 간섭 효과로 방사율에 영향을 줌

   5. 시야각(Viewing angle)은 특히 반사 표면에서 방사율에 영향을 줌

출처

- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653

- Salisbury, J. W., Wald, A., & D’Aria, D. M. (1994). Thermal-infrared remote sensing and Kirchhoff’s law: 1. Laboratory measurements. Geophys. Res., 99(B6), 11897–11911. https://doi.org/10.1029/93JB03600

- Warren, T. J., Bowles, N. E., Donaldson Hanna, K., & Bandfield, J. L. (2019). Modeling the angular dependence of emissivity of randomly rough surfaces. Journal of Geophysical Research: Planets, 124, 585–601. https://doi.org/10.1029/2018JE005840

- Zhang, Z., Chen, M., Zhang, L. et al. (2023). A straightforward spectral emissivity estimating method based on constructing random rough surfaces. Light Sci Appl, 12, 266. https://doi.org/10.1038/s41377-023-01312-1

- Chang-Da Wen, Issam Mudawar (2006). Modeling the effects of surface roughness on the emissivity of aluminum alloys. International Journal of Heat and Mass Transfer, 49(23–24), 4279–4289. https://doi.org/10.1016/j.ijheatmasstransfer.2006.04.037

- Agababov, S. G. (1968). Effect of the roughness of the surface of a solid body on its radiation properties and methods for their experimental determination. High Temperature, 6, 76–85.